Y Combinator ,C++ and so on
first saw
在之前的文章中我实现了一个可递归的lambda表达式,但是并不严谨,一个严谨的递归匿名函数应该是Y组合子.
它能将任何形式的函数递归调用转换为匿名函数递归调 用。 这个式子就被成为Y组合子,它的作用就是实现匿名函数的递归自调用.
Y组合子是一个很有趣的概念,很多人认为Y组合子是函数式编程的重要组成部分之一.
… we can similarly use knowledge of the Y combinator as a dividing line between programmers who are “functionally literate” (i.e. have a reasonably deep knowledge of functional programming) and those who aren’t.
那用c++来实现Y组合子如何?

让我们先用Lambda Calculus引入
Lambda Calculus
先从最简单的lambda表达式开始
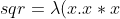
BNF语法
<expr> ::= <identifier>
<expr> ::= lambda <identifier-list>. <expr>
<expr> ::= (<expr> <expr>)
我们把这个表达式写成代码
Haskell
sqr = \x -> x * x
scheme
(define sqr ( lambda (x) (* x x) ))
这是一个很简单的表达式, 在c++中可写成
[](int x) {return x * x};
进一步 我们限定一个范围
[](int x)->int {return x * x};
用function打包一下
function<int(int)> const sqr =
[](int x)->int {return x * x};
现在你已经会了解简单的匿名函数了,下面我们来介绍 Fixed-point(不动点)
Fixed-point Combinator
一个Fixed-point Combinator是一个高阶函数,可被写成 \(yf = f(yf)\) 可以很轻易的看出来这个表达可以不断嵌套,如果是已经确定的函数,那么我们就可以直接写出一个递归的函数了(而且不用递归的方式(逃))
一个经典的例子是阶乘
fact n = If IsZero n then 1 else n × fact (n − 1)
改写成yf的样子
很容易写成 F f n = If IsZero n then 1 else n × f (n − 1)
我们在haskell中试着去实现这个
fix f = f (fix f)
fact = fix $ \ f n -> if (n == 0)
then 1
else n * f (n - 1)
很明显的,我们利用了haskell的惰性求值,在没有惰性求值特性的语言下能成立吗?
我们先完成一个在lazy-scheme 上能跑的程序
(define Y
(lambda (f)
(f (Y f))))
(define F
(lambda (f)
(lambda (n)
(cond
((eq? n 0) 1)
(else (* n (f (- n 1))))))))
(define fact (Y F))
#简单的翻译
我们这个地方需要applicative-order 而不是 normal-order,在成为参数前,lambda表达式的值不会被计算
https://latex.codecogs.com/gif.latex?f=%3E\lambda%20x.fx
这样可以实现一个applicative-order的展开
(define Y
(lambda (f)
(f (lambda (x) ((Y f) x)))))
很好,它可以在strict Scheme(我测试的mit-scheme)上跑的起来
现在实现C++版本的
#include <iostream>
#include <functional>
using namespace std;
template <typename T, typename R>
function<R(T)> Y(
function<function<R(T)>(function<R(T)>)> f)
{ // Y f = f (λx.(Y f) x)
return f([=](T x) { return Y(f)(x); });
}
typedef function<int(int)> fn_1ord;
typedef function<fn_1ord(fn_1ord)> fn_2ord;
fn_2ord almost_fact = [](fn_1ord f) {
return [f](int n) {
if (n == 0)
return 1;
else
return n * f(n - 1);
};
};
int main()
{
fn_1ord fact = Y(almost_fact); //wrapper
cout << "fact(5) = " << fact(5) << endl;
}
Y Combinator
Y = \lambda f.(\lambda x.f(xx))(\lambda x.f(xx))
我们正式的来完成一个Y-combinator,
把YF拆解一下
Y F= \lambda f.(\lambda x.f(xx))(\lambda x.f(xx))F
\\=(\lambda x.F(xx))(\lambda x.F(xx))
\\=F(YF)
(define Y
(lambda (f)
((lambda (x) (x x))
(lambda (x) (f (lambda (y) ((x x) y)))))))
用fix-point改写一下的结构
现在差最后关键的一步, 在scheme中我们能这样定义函数
(define Y
...
lambda( (y) ( (x x) y) )
)
但是在c++里面并不行,让我们打包一下函数本身
template <typename F>
struct self_ref_func {
function<F(self_ref_func)> fn;
};
template <typename T, typename R>
function<R(T)> Y(
function<function<R(T)>(function<R(T)>)> f)
{ // Y = λf.(λx.x x) (λx.f (λy.(x x) y))
typedef function<R(T)> fn_1ord;
typedef self_ref_func<fn_1ord> fn_self_ref;
fn_self_ref r = {
[f](fn_self_ref x)
{ // λx.f (λy.(x x) y)
return f(fn_1ord([x](T y)
{
return x.fn(x)(y);
}));
}
};
return r.fn(r);
}
最后写成c++,现在已经完成了简单的实现了